Arduino Line Following Robot: Cracking the shortest/fastest path on a grid with loops

I'm sure you've created a line following robot at some point, if you've been exposed to Arduino (or any other programmable electronics in general). And most of the time, the next step is to make the robot learn the shortest path from one point to another in a line maze. This was a part of the mission given in a robotics competition once held at our company. Well, competitions are my thing :) 

So I built a line following robot using Arduino but when I was trying to figure out how to navigate a grid with loops, I could not find any useful online materials regarding the topic. Almost all materials were about non-looped grids and navigation was based on LSRB Algorthm which does not work out-of-the-box with looped grids. So I had to code one on my own and it was an exciting project to be involved during the "Stay At Home" time due to #COVID19 outbreak. But this isn't a rambling on my robot build (I'll save that for later). This is rather a theoretical walkthrough of how I cracked the shortest path problem.

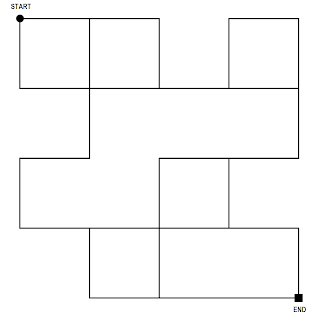
The grid shown above is a simplified version of what our competition ran on. Maybe the maze that you have to crack has deadends, skewed angles or irregular path lengths and you might think this approach won't work for you. But if you closely look at a maze with deadends and whatnot, you'll understand that it can be simplified to something close to the above once the robot finishes its learning phase.

Let's establish some notations before we go any further.

N - North, S - South, W - West, E - East.

If you look at the above grid, what could be the shortest path in your book? The end node can be reached by travelling through 10 sections at a minimum. In fact, there are a total of 9 unique paths that have exactly 10 sections from start to end. I've marked 3 of them on the below grid with different colours. Which one out of these 9 paths would you rather choose?

1. S,E,E,E,E,S,W,S,E,S

2. E,S,E,E,E,S,W,S,E,S

3. E,E,S,E,E,S,W,S,E,S

4. S,E,S,W,S,E,S,E,E,E

5. S,E,S,W,S,E,E,S,E,E

6. S,E,S,W,S,E,E,E,E,S

7. E,S,S,W,S,E,S,E,E,E

8. E,S,S,W,S,E,E,S,E,E

9, E,S,S,W,S,E,E,E,E,S

Well, who cares? As long as you take any one of them, it would still be the shortest path since they all have the same length, right? Well, technically it is, but practically not so much. Let me elaborate.

If you are only doing a mathematical calculation of the shortest path, either solution would suffice but in reality, you are building a line following robot that needs to navigate from start to end. Following the line is not the hard part. Turning is! 

Turning warrants your robot to slow down, break away from your line following algo, spin wheels in an unorthodox manner, make sure the timing is right and the wheels won't slip and if you are really crazy it could even mean to employ a compass to post validate the turn or a failsafe algo to reverse the robot back to its previous junction and start over again in case it messes up the turn.

Well, that escalated quickly! Whatever.

The point is, a turn in your path wastes a lot of time and resources and is prone to many errors when performed. It's too costly, especially in a competition setup where you need to get to the end node as fast as you can. Sometimes, the fastest path may even be longer than the shortest path! Food for thought :)


Not all shortest paths are equally fast
Let's have a re-look at the shortest paths we came up with.

1. S,E,E,E,E,S,W,S,E,S - 6 turns

2. E,S,E,E,E,S,W,S,E,S - 7 turns

3. E,E,S,E,E,S,W,S,E,S - 7 turns

4. S,E,S,W,S,E,S,E,E,E - 7 turns

5. S,E,S,W,S,E,E,S,E,E - 7 turns

6. S,E,S,W,S,E,E,E,E,S - 6 turns

7. E,S,S,W,S,E,S,E,E,E - 6 turns

8. E,S,S,W,S,E,E,S,E,E - 6 turns

9, E,S,S,W,S,E,E,E,E,S - 5 turns

What does this new information tell you? It tells you that there is actually an optimal path for the robot to take, although you couldn't see it previously because you only considered the "length" when calculating the "shortest path".

So how do we calculate the shortest path which has the least number of turns? The general shortest path algorithms like Dijkstra or A* does not help in this sense as they do not offer multiple path choices at the end of their calculations. All they present us is a single solution and we have to accept it, no questions asked. If you dig deep, you'll notice that A* won't even be a suitable candidate to solve our problem. Then what?

Dijkstra with a twist

You guessed it right. Let's see if we can tweak the age-old Dijkstra's algo to suit our needs. If you don't remember it, watch this video first.

The algo is just fine in its own right but it keeps discarding the successive paths which have the same minimum cost to a node, which leads us to miss other options of arriving at a node at the same cost. So how do we solve this? Well, when you implement the algo in your code, instead of keeping one reference to the previous node, use an array of references to store multiple values.

Remember, this post is more or less a theoretical walkthrough of my approach. So don't expect me to spit out working code samples on the way. But that doesn't mean these concepts are unrealistic. I built my robot on them and it performed unimaginably well.

To implement what we just talked about, you need to structure your node somewhat similar to the following:

Node {

    Int X;

    Int Y;

    List Neighbours;

    List PreviousNodes;

    Int Cost;

}

Note that X,Y and Neighbours should be populated before you try to find the shortest path. That should happen during the learning phase, where your robot traverses the grid to understand all node positions (X,Y) and their neighbours. It is a problem domain on its own and not discussed in this post, but I'll probably be covering that in a future post - may be as a sequel.

With Dijkstra, you need to do a breadth-first grid traversal starting from a given node. For that, you need to recursively traverse their neighbours while storing their costs and their previous node references. The PreviousNodes property can be used to determine whether there is a turn involved when taking the path towards its neighbours. Let's see how.

Consider the following state of nodes after a few iterations:

NodeA(X=0, Y=0, Neighbours(NodeB, NodeC), PreviousNodes(), Cost=0)

NodeB(X=1, Y=0, Neighbours(NodeA, NodeD, NodeE), PreviousNodes(NodeA), Cost=10)

NodeC(X=0, Y=1, Neighbours(NodeA, NodeD), PreviousNodes(NodeA), Cost=10)

NodeD(X=1, Y=1, Neighbours(NodeB, NodeC, NodeF, NodeH), PreviousNodes(NodeB, NodeC), Cost=20)

Don't worry much about how the PreviousNodes or the Cost property was populated for the above nodes, I'll get to that later. Right now we are going to consider NodeD as our current node and continue the iteration. We need to calculate the costs of NodeD's neighbours. NodeB & NodeC are already processed so we can skip those. We only need to consider NodeF & NodeH.

Since the grid is made of squares, cost between any two adjacent nodes is the same. For calculation, we can take it as 1, but since we are going to do some tweaks, take it as 10 instead. It doesn't really matter what number you use, as long as it's the same for all. I hope the assigned costs for nodes from A-D make sense now.

Now take the neighbour NodeH. Its cost would be calculated as 30 (NodeD cost) + 10. But NodeD has two previous nodes which both amount to a cost of 20. But if you arrive at NodeH via NodeB instead of NodeC, you don't have to turn at NodeD. So going via NodeH as A-B-D-H is faster than going via another competitive node like NodeF as A-B-D-F (Bad example though, NodeF also has a comparable path through A-B-E-F but just ignore that for the moment). So when you mark the cost of NodeH, mark it as 29 instead of 30.

You may decide what the deduction amount should be. It all depends on how costly your turns are and how far apart your nodes are. If the fixed cost is 10 and the deduction is 5, it sort of means your robot takes the same amount of time to make a turn and to drive half-length between two nodes.

If you keep on calculating the node costs using this method, eventually you'll end up with a cost matrix that gives you the shortest path via the No. 9 route which only has 5 turns.

Although, there's a small caveat which you need to be aware of when you are constructing the shortest path. With Dijkstra, you have to backtrack from the end node, all the way to the starting node, but now you have multiple previous nodes to deal with.

When a node has multiple previous nodes, loop through them and pick the one which does not change your current direction of travel. If both changes it, there is no harm picking either one. The complete cost matrix is shown below. I hope it is self-explanatory.

That's basically it :)